.

Dr. Nicholas J. Matzke started out as geography grad student at the University of California in Santa Barbara who had obvious passions outside of geography. He then went on to become fairly well-known debating on Talk.Orgins.org, where I first ran into him myself and had several lengthy discussions. Since then, Nick has made a real name for himself. He is the former Public Information Project Director at the National Center for Science Education (NCSE) and served an instrumental role in NCSE’s preparation for the 2005 Kitzmiller v. Dover Area School District trial. One of his chief contributions was discovering drafts of Of Pandas and People which demonstrated that the term “intelligent design” was later substituted for “creationism”. This became a key component of Barbara Forrest’s testimony. After the trial he co-authored a commentary in Nature Immunology, was interviewed on Talk of the Nation, and was profiled in Seed magazine as one of nine “revolutionary minds”.
Matzke has written many in-depth pieces and has made frequent posts online, including regularly blogging at The Panda’s Thumb. He wrote a lengthy paper about the evolution of flagella and has challenged intelligent design claims that flagella are irreducibly complex. He co-authored a critique of Stephen C. Meyer’s paper that became important in the Sternberg peer review controversy. He also critiqued Jonathan Wells’ book Icons of Evolution and contributed to NCSE’s book Not in Our Classrooms.

Nick is currently a postdoctoral fellow at the National Institute for Mathematical and Biological Synthesis. He received his Ph.D. in evolutionary biology at the University of California, Berkeley in 2013.
So, given his distinguished background, I welcome his recent contribution to this forum.
This particular discussion is taken, with some modifications, from the comment section of Dr. Jason Rosenhouse “Among the Creationists“- a review of my recent live radio debate with Dr. Rosenhouse.
________________________
Hi Nick, welcome back.
You write:
Your arguments and probability calculations are based on the effects of many simultaneous mutations, with no opportunities for selection between them. Thus, under your model, large moves in sequence space have to happen all-at-once. Your criticisms of that model are valid, but they say nothing about the evolutionary model, which is stepwise.
 You seem to have a mistaken view of sequence space, islands within sequence space, and how mutational changes can move around within this space. To illustrate the problem here, imagine that our population starts out on an island within a higher level of sequence space (i.e., 1000 aa sequence space with a moderate specificity requirement). This island is made up of many protein sequences that can all produce the same qualitative type of function to at least some selectable advantage. Along the edges of the island are sequences that are marginally beneficial while in the center of the island are sequences that are strongly beneficial for the particular type of function in question (creating a peak for the island with exponentially declining slopes toward the surrounding ocean). Surrounding this island, on all sides, are sequences that are not beneficial at all. They may be functionally detrimental to one degree or another, or they may be functionally neutral, but they aren’t selectably beneficial.
You seem to have a mistaken view of sequence space, islands within sequence space, and how mutational changes can move around within this space. To illustrate the problem here, imagine that our population starts out on an island within a higher level of sequence space (i.e., 1000 aa sequence space with a moderate specificity requirement). This island is made up of many protein sequences that can all produce the same qualitative type of function to at least some selectable advantage. Along the edges of the island are sequences that are marginally beneficial while in the center of the island are sequences that are strongly beneficial for the particular type of function in question (creating a peak for the island with exponentially declining slopes toward the surrounding ocean). Surrounding this island, on all sides, are sequences that are not beneficial at all. They may be functionally detrimental to one degree or another, or they may be functionally neutral, but they aren’t selectably beneficial.
Now, say our population happens to land on the edge of such an island. A selectable advantage is suddenly realized. So, this population will be preferentially maintained by natural selection. After this point, it is very easy to move the population rapidly up the slopes of the island to the very peak of the island in relatively short order (which has the effect of reducing the size of the island that will be considered “beneficial” for the population by natural selection). The reason for this is that the sequences with a stepwise increase in selectability are very closely spaced on this island. So, improving functionality of a given type on a particular island isn’t a problem for RM/NS – even by mutations that only produce single character changes (point mutations).
 The problems, of course, happen when one tries to leave the island and find other islands within sequence space. In order to do this, mutations, of various types, start to explore the sequences in the ocean around the island. Point mutations take very small steps off the island. If these point mutations land on neutral (or near neutral) areas of the ocean, they are not immediately deleted by natural selection. They can wander around a bit looking for other islands along a “random walk”. If these point mutations land on strongly detrimental regions of the surrounding ocean, natural selection quickly deletes them and the random walk starts over from the starting island. Of course, this “start over” process takes time.
The problems, of course, happen when one tries to leave the island and find other islands within sequence space. In order to do this, mutations, of various types, start to explore the sequences in the ocean around the island. Point mutations take very small steps off the island. If these point mutations land on neutral (or near neutral) areas of the ocean, they are not immediately deleted by natural selection. They can wander around a bit looking for other islands along a “random walk”. If these point mutations land on strongly detrimental regions of the surrounding ocean, natural selection quickly deletes them and the random walk starts over from the starting island. Of course, this “start over” process takes time.
Now, imagine a scenario where the next closest beneficially selectable island in sequence space is a Hamming distance of 50 non-selectable mutations (character changes) away from the starting island within a sequence space that holds 1000 character sequences. How long would it take to get to that next island? Say that your population on the starting island is at a steady state of 1e31 (the size of the number of all the bacteria on Earth). Say that our mutation rate is one mutation per 1000 character sequence per generation, and our generation time is 10 minutes. The number of non-beneficial sequences within a Hamming distance of 50 within this sequence space is ~1e65. Given these parameters, our population could explore a maximum of 1e31 sequences within the surrounding ocean in each generation. Of course, this means, on average, that it would take our population about 1e34 generations, on average, to reach an island that is just 50 character differences away from the starting island (i.e., ~1e29 years).
But, you argue, any mutations that are detrimental will be selected against my natural selection, which is true. However, this doesn’t improve the odds of success. All natural selection does in such a case is bring back to random walk sequence to the original starting island. The effect that this has is to increase the searches very close to the starting point island. However, it doesn’t really help to find something that is 50 mutational steps away any faster. If anything, it increases the average number of mutations required to achieve success.
 Of course, this is why Jason Rosenhouse argued that there were these nice little paths of closely-spaced sequentially selectable steppingstones in higher-level sequence space – and why you claimed that this is in fact the true view of sequence space. Unfortunately, this view isn’t supported by what is actually known of sequence space where the steppingstones are randomly scattered throughout in a fairly uniform manner.
Of course, this is why Jason Rosenhouse argued that there were these nice little paths of closely-spaced sequentially selectable steppingstones in higher-level sequence space – and why you claimed that this is in fact the true view of sequence space. Unfortunately, this view isn’t supported by what is actually known of sequence space where the steppingstones are randomly scattered throughout in a fairly uniform manner.
So, in this light, let’s consider the rest of your specific arguments:
This doesn’t matter, since in evolution, all the mutations don’t occur at the same time. Each is exposed to long periods of selection, drift, etc. The real process is that after a substitution happens in a population (either beneficial, beneficial but with some negative side effects, or neutral, or nearly neutral but slightly deleterious), a variety of new mutations accumulate over subsequent generations. Some of these mutations are neutral, some are slightly deleterious, and some compensate for some deleterious feature introduced by a previous substitution. Compensatory substitutions, in particular, are crucial to include in the model. Creationist arguments, including yours, universally ignore the role they play.
My model does not ignore compensatory mutations at all. The effect of compensatory mutations is simply to reverse the random walk of a sequence back onto the original island from which it started. That’s all. Compensatory mutations do not help to reduce the average time required to find a qualitatively novel island within sequence space.
You’re not getting the basics. After a slightly deleterious substitution, followed by a compensatory mutation, you are not returning to where you started, you have moved to a different place in sequence space. The compensatory mutation makes the sequence more different from the original sequence, not more similar to it. The “space” we are talking about is sequence space, unless you want to abandon all your previous arguments.
This is certainly basic stuff here…
Consider that compensatory mutations maintain the same function at the same or, more often than not, at an improved but still reduced level of original functionality by compensating, with a different mutation, for a detrimental mutation that came before. All such compensations therefore relocate the evolving sequence back onto the very same starting island – an island, as already explained to you, that is comprised of a cluster of all sequences that can produce the same basic structure with the same original function in question. So, even though a compensatory mutation produces a different sequence compared to the original, the new sequence is still on the very same starting island of sequences. It’s just on little different spot on the same island – not a different island. It’s like taking a step off the beach and into the water and then back onto the beach again a couple feet or so away from where you first stepped off the beach. Big deal! It’s lovely that you’ve figured out how to walk all around the beach of the very same island, but how does this ability reduce the time it takes to actually swim, blindly, to the next closest island that has a qualitatively different type of function?
This is why compensatory mutations don’t help reduce the time required to find a new island. They just help sequences to stay on the same starting island is all. It is for this reason that natural selection is a preserving force, not a creative force beyond very low levels of functional complexity.
Beyond this, I’ll point out that I’m not arguing that mutations need to occur at the same time. They don’t. Mutations can and generally do occur one at a time and are generally comprised of single-character mutations. Multi-character mutations (indels) can also occasionally occur, and these types of mutations can make long leaps into the ocean of sequence space, far away from the original island. However, the odds of successfully landing on any part of any other island within sequence space are not statistically improved. The average time to success is still the same either way.
Also, proteins are much more flexible than, say, English. It is commonplace to find protein families where 50% or even 80% of the amino acids have changed, yet the structure and function remain the same. Not so for English. Protein evolution is more like language evolution, where most / all of the words can be modified, the resulting languages are incomprehensible to each other, but the same message can be communicated via different sentence, each within the overall context of its language.
There are two different concepts here. One is that unrelated sequences can occasional perform the same type of function (as with my “black horse” example listed below). But, I don’t think this is the argument you’re trying to make here. It seems like you’re arguing that the same basic structure/function can be achieved by selectively changing numerous amino acids in a protein along with compensatory changes to other parts of the protein. And, this is true. It all depends upon the degree of protein specificity. Take, for example, an average sized protein of 300aa. Most of the amino acid residue positions in this protein can be changed, at the same time, without a complete loss of function. However, there is a limit to how they can be changed. Some residue positions can be changed into almost any of the other 19 residue options without a significant affect on function. Other residue positions can only be changed within a certain class of residue options (hydrophilic vs. hydrophobic, etc.). And, some residue positions are highly constrained, only allowing one or two different residues to occupy that spot.
What this flexibility means, of course, is that you’re correct – most protein-based systems can in fact realize a change of “50% or even 80%” of their amino acid residue positions without a significant loss of structure or function. However, this argument misses the fact that relative to the overall size of sequence space, the constraints of the minimum specificity requirements on the protein-based system in question means that only the tiniest fraction of all possible sequences can given rise to that particular type of protein-based system/function. And, beyond this, this ratio decreases exponentially as the minimum size and/or specificity requirements increase in a linear manner.
You seem to view protein flexibility as somehow creating steppingstones across sequence space. This view is incorrect. Sequence space is hyperdimensional. All of the sequences that make up a particular functional system/structure within sequence space are part of the same island complex – the same steppingstone. They are not part of different steppingstone islands. Getting from one island to the next closest beneficial island that actually has a qualitatively unique function requires that one get off the starting island and explore the surrounding sequence space that does not reside on the starting cluster of island sequences. And, the likely success of this effort, via RM/NS is dependent upon the ratio of potentially beneficial vs. non-beneficial sequences in sequence space that exist outside of the original starting point island of sequences. And, what may seem to you like closely spaced steppingstones in sequence space when imagining hyperdimensions projected onto two or three dimensional space, are really very widely spaced steppingstones when viewed in their correct hyperdimensional context.
Your arguments are rather like arguing that French and Romanian could not have evolved from a common ancestor, because if you take a French sentence and randomly mutate most of the letters in each of the words, you get something incomprehensible. This is nothing like the actual proposed historical process, and so is not a rebuttal of it. Language space is surely huge just like sequence space, and it is surely true that most random assemblages of sounds don’t mean anything in any modern or extinct language, yet languages have evolved nonetheless, through a long process of step-by-step changes, with the participating humans mostly or completely oblivious.
This is a mistaken analogy for several reasons. The first is that humans are intelligent and can make leaps within sequence space that cannot be made by random mutations in a comparable amount of time. Also, humans can assign meaning to any random sequence of letters at will. Nature cannot do this with protein-based sequences. And, single-word sequence space simply isn’t very large. Single words are actually quite closely spaced together within sequence space. It isn’t until you start talking about longer sentences and paragraphs that the ratio of potentially meaningful/beneficial vs. non-beneficial gets too sparse for any mindless search algorithm to be successful in a reasonable amount of time. This is why books, essays, journals, and computer codes, regardless of the human language used, do not evolve via the same mechanism as Darwinian evolution. Such “evolution”, if you want to call it that, is guided by intelligence.
Beyond this, different human languages are effectively the same with the exception that different letters and words are used to represent the very same ideas. Other than that, all human languages work in the very same way. Words are used to make sentences and sentences to make paragraphs and paragraphs to make longer articles, essays, or books – along a continuum of higher and higher levels of functional complexity. All of these higher levels of functional complexity are realized by intelligent design – for all human language systems (to include computer codes and languages). A mechanism of random mutations and function-based selection could never produce even lower levels of functional complexity in nearly so short an amount of time and could never produce the higher levels of functional/meaningful complexity this side of a practical eternity of time.
Protein-based systems can also be viewed as being based on basic “words” or word-type sequences as well as phrases, paragraphs, essays, etc., along a continuum of functional complexity from lower to higher levels. Note, however, that the problems for evolutionary progress from lower to higher level systems is the same for human languages as it is for protein-based systems. As in the human-language system, there are many possible ways of saying the same thing. For example, I could say, “That’s my black horse.” or I could say, “The ebony steed is mine.” These are different ways of getting essentially the same idea across. The mode of “English” is equivalent to the environment. Saying the same thing in a different language, like Russian, wouldn’t make sense in an English-speaking environment. And, the same thing is true for protein-based systems. Their useful function is dependent upon the surrounding environment.
However, these many possible ways of saying the same thing get farther and farther apart in sequence space as the thing that is trying to be said increases in the minimum required number of characters that have to be used to get the desired idea across. The very same thing is true of protein-based systems. While there are many very different options for producing the very same type of system (such as many unique types of bacterial flagellar motility systems), these options become more and more widely spaced in sequence space with each step up the ladder of minimum structural threshold requirements. That is why it doesn’t matter what “language” one uses. Regardless, one cannot get from a given higher level island within sequence space to any other (regardless of the “language” that would be recognized in a given environment) in a reasonable amount of time.
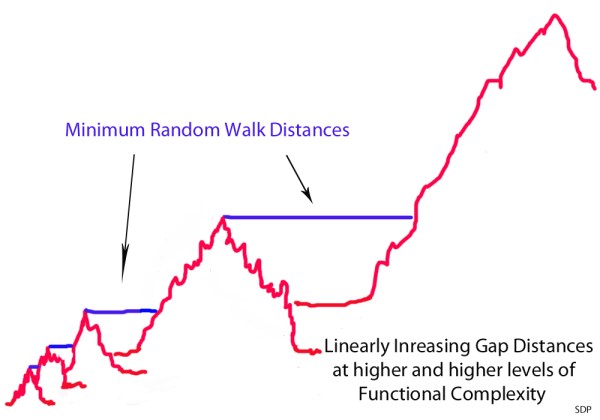
Another problem here is that you seem to imagine that going from lower-level to higher-level systems is a smooth process where there are no significant gaps between lower-level and higher-level islands within different levels of sequence space. That’s just not a correct vision of sequence space (human language or otherwise). The lower level islands are also separated from higher level islands by gaps comprised of non-beneficial sequences. And, these minimum gap distances become linearly wider and wider with each step up the ladder of functional complexity (see the illustrations a the end of this article).
Other examples of this mistake in your comment:
The reason for this is because there is an “experimentally observed exponential decline in the fraction of functional proteins with increasing numbers of mutations (Bloom et al. 2005).”
…and again:
Bloom goes on to point out that, “Experiments have demonstrated that proteins can be extremely tolerant to single substitutions; for example, 84% of single-residue mutants of T4 lysozyme and 65% of single-residue mutants of lac repressor were scored as functional. However, for multiple substitutions, the fraction of functional proteins decreases roughly exponentially with the number of substitutions, although the severity of this decline varies among proteins.”
…and again:
In short, most mutations that affect a region or island cluster of thermodynamically stable sequences in sequence space are destabilizing in such a way that each additional mutation has an exponentially destabilizing effect. Obviously, this means that the vast majority of sequences in sequence space would not produce viably stable proteins.
It is true that most mutations have this effect, but this doesn’t matter, since they happen for the most part one at a time, and (1) selection removes the severely deleterious mutations, and (2) the slightly deleterious ones can later be corrected by compensatory substitutions.
While both of your points here are true, they really don’t help to lessen the average time required to find a novel beneficial island within sequence space (as already explained). My point in referencing the experiments of Bloom et. al. was to show how the islands of beneficial sequences actually appear in sequence space. They are islands with steep slopes and fairly sharply pointed peaks – as I originally explained. The degree of protein flexibility that you point to really doesn’t solve this problem – as noted above.
The “vast majority of sequences” therefore don’t matter, since evolution doesn’t have to search through all possible sequences in order to explain the data. To explain the data, it just has to, *sometimes*, find *some* of the paths between proteins with different-but-related sequences but the same function, and, occasionally, find *some* of the paths between proteins with different-but-related sequences and different functions. It doesn’t have to do it *all* the time for *everything*, because the data indicates that failures are common (extinctions are observed, imperfect adaptations are observed), and the data indicate that biology doesn’t occupy all of functional space or sequence space, just little bits of it.
There are two misconceptions here. The first is, as already explained, that moving around between sequences that are located on the same island with the same type of function is very easy for RM/NS. This is not a problem whatsoever. However, moving around on the same island doesn’t get you to a new island with a new type of function – which is what our discussion is about.
Now, you also claim that “occasionally” some of the paths between “different-but-related protein sequences” can be found with “different functions”. This is the entire question at hand. What is the average expected time for such a feat to be realized? – at various levels of functional complexity? You simply don’t know since you believe that, regardless of the level of functional complexity, that closely-spaced steppingstone islands exist somewhere in sequence space whereby random mutations can actually get from one novel island to the next without having to make much of a random walk. This claim of yours (identical to the claim of Jason Rosenhouse), simply doesn’t reflect what is known about sequence space at various levels of functional complexity. There simply are no such closely-space islands at higher levels of functional complexity that are actually known, and no reason to think that such a situation will ever be discovered.
But, you write, “The data indicate that biology doesn’t occupy all of functional space or sequence space, just little bits of it.”
That’s just the point. Since even a very large population can only occupy the tiniest fraction of sequence space at a higher level of functional complexity, the finding of novel islands at the same level or higher involves crossing vast gaps of non-beneficial sequences that do in fact exist between each one of these higher-level islands and the next closest island. And that, my friend, is the fundamental problem for the ToE.
It also suggests that as sequence space increases in size by 20^N, the ratio of viable vs. non-viable sequences, not just systems, decreases exponentially. – Sean Pitman
This is just the all-at-once fallacy repeated again.
No, it isn’t. What it means is that your one-at-a-time mutations simply cannot cross the resulting gap distances in a reasonable amount of time beyond very low levels of functional complexity. It’s the very same problem regardless of if there are many random mutations at a time or just one random mutation at a time. The odds of success are the same.
You conclude with:
And, this effect only gets exponentially worse and worse with each step up the ladder of functional complexity. – Sean Pitman
This is raw assertion, not something your references say, and you haven’t defined the “ladder of functional complexity” anyway. Most of protein complexity involves fusing protein domains or evolving binding sites between them, these are pretty trivial processes.
I have defined the “ladder of functional complexity” (as have others in literature) as the minimum size and specificity of the parts required to produce a given type of function. In other words, some protein-based systems have a minimum amino acid residue requirement of only a dozen or so specifically arranged residues, while other protein-based systems have a minimum requirement of several thousand specifically arranged residues. These systems are on very different levels of functional complexity. And, the sequences spaces needed to hold these different systems are also very different when it comes to the ratio of beneficial vs. non-beneficial and the resulting distances between the beneficial islands of proteins within these sequence spaces.
See the table at Panda’s Thumb from Pallen & Matzke 2006. There is a lot more to the argument than just the 10 proteins homologous to nonflagellar T3SS.
I do extensively discuss your 2003 paper, “Evolution in (Brownian) space: a model for the origin of the bacterial flagellum“.
It seems to me that they key difference you see between your 2003 and your 2006 papers is the discovery of more homologies for vital structural flagellar proteins. You write:
The important overall point, as discussed in my blog post, is that of the 42 proteins in Table 1 of Pallen and Matzke, only two proteins, FliE and FlgD, are both essential and have no identified homologous proteins. This is substantially more impressive than the situation in 2003, and means that the evidence for the evolutionary origin of the flagellum by standard gene duplication and cooption processes is even stronger than in 2003. (Link)
You see, I really don’t care if every single one of the individual protein parts within the flagellum are homologous to proteins within other systems (even though a couple of them are not currently known to be homologous to anything else). This is completely irrelevant to the plausibility of the evolution of higher level systems based on pre-existing subsystems. You see, the problem is that having all the required parts to make a new type of complex system isn’t enough. Why not? Because, these parts must be modified in very specific ways before they can work together in a new specified arrangement as parts of a different type of complex system – like a flagellar motility system. And, the number of required modifications to get the parts in your proposed pathway to work together, to any selectable advantage at a higher level of functional complexity, is simply too great to be realized this side of a practical eternity of time.
How is that? After all, is it not possible for the required parts to be perfectly homologous between different systems? Well no, it’s not. If this were the case, all kinds of very different complex systems could be produced using identical subparts. The reason why this doesn’t happen is because qualitatively different complex systems require key modifications for the otherwise homologous parts to work together in different ways (Link). And, the great the number of these required non-selectable modifications to otherwise homologous parts, the exponentially greater the average random walk time. So, by the time you’re at a level when the minimum number of required non-selectable modifications is a couple dozen or so, the average time to randomly produce all of these required modifications, which cannot be guided by natural selection, is trillions upon trillions of years. And, I fail to see how compensatory mutations help to solve this problem? As far as I can tell, they do nothing to solve this problem for the ToE.
In short, homologies simply don’t cut it because the similarities are not what’s important when it comes to understanding evolutionary potential and/or limitations. What is important here is an understanding of the number of required non-selectable modifications. These required, non-selectable, modifications are what completely kill off evolutionary potential, in an exponential manner, beyond very low levels of functional complexity.
For a further discussion of your flagellar evolution arguments see: http://www.detectingdesign.com/flagellum.html
There is no point in discussing this until we resolve your misconception about the ability of single proteins to evolve along narrow paths through huge sequence space, in some cases retaining the same function, in other cases changing function.
Those paths exist. Phylogenies of proteins are one of the proofs. The branches of the phylogenies are actual statistical estimates of these paths. They exist both for cases where all the proteins at the tips have the same function, and for cases where some of the proteins at tips of the tree have different functions.
Phylogenies say nothing of the gap distances between the proposed steppingstones and how the distance between these steppingstones can be traversed along “narrow paths” via random mutations – which is the key problem with your flagellar evolution papers. You simply wave your hand and blindly assume that the gap distances are small enough because of the phylogenetic “relationships” or similarities between proteins within different systems. You see, the problem isn’t with the similarities. The problem for your mechanism is with the number of required non-selectable differences to get from one system, from one steppingstone, to the next. Phylogenetic similarities do suggest a common origin of some kind, but they do not tell you that the mechanism of RM/NS was in fact capable of producing the required differences – a key mistake on the part of evolutionists such as yourself.
For example, the steppingstones you list off in your flagellar evolution pathway are each far too far apart in sequence space for random mutations to get from any one to any other in a reasonable amount of time. The required non-selectable changes are simply far far too numerous for your theory to be tenable. Beyond this, as confirmation of this problem, not one of your proposed steps from one steppingstone to the next has been demonstrated in the lab. If these steppingstones are truly as close together as you seem to imagine, such a demonstration should be no problem. Take the wild-type system for one steppingstone and show how, given the appropriate selective environment, the next steppingstone in your suggested evolutionary sequence is actually reachable in what anyone would call a reasonable amount of time.
 The only thing that has been convincingly demonstrated is that one of your proposed steppingstones, a T3SS, devolved from a fully formed flagellar motility system – not the other way around. This is right in line with predictions of intelligent design where the devolution of a complex system into less complex subsystems is very easy (like a car that has lost its tires, but the headlights still work – like a giant flashlight). As a real life example, consider the case of blind cavefish that lose the ability to grow eyes because of a relatively small mutation that turns off the eye genes in these fish – genes which remain largely intact and can be turned on by one or two reversion or compensatory mutations if the environment changes so that eyes would once again prove beneficial. Such are examples of devolution, not evolution, in action. Try turning it around and going the other way, as you suggest. It just doesn’t happen. Downhill evolution is far far easier than uphill evolution because of the exponentially expanding problem of non-beneficial gaps, between each potential steppingstone, with each step up the ladder of functional complexity.
The only thing that has been convincingly demonstrated is that one of your proposed steppingstones, a T3SS, devolved from a fully formed flagellar motility system – not the other way around. This is right in line with predictions of intelligent design where the devolution of a complex system into less complex subsystems is very easy (like a car that has lost its tires, but the headlights still work – like a giant flashlight). As a real life example, consider the case of blind cavefish that lose the ability to grow eyes because of a relatively small mutation that turns off the eye genes in these fish – genes which remain largely intact and can be turned on by one or two reversion or compensatory mutations if the environment changes so that eyes would once again prove beneficial. Such are examples of devolution, not evolution, in action. Try turning it around and going the other way, as you suggest. It just doesn’t happen. Downhill evolution is far far easier than uphill evolution because of the exponentially expanding problem of non-beneficial gaps, between each potential steppingstone, with each step up the ladder of functional complexity.
In short, based on your Panda’s Thumb website, here’s how evolution is supposed to climb up the mountains (higher levels of functional complexity) in the fitness landscape of sequence space:
However, in reality, this is what happens:
The minimum non-selectable Levenshtein distances between the peak of one mountain and the next closest beneficially selectable sequence with qualitatively novel functionality increases linearly with each step up the ladder of functional complexity. It’s kind of like a fractal where the the only think that changes is the scale. However, this change in scale has a dramatic effect on the average random walk time at different scales. With each linear increase in the minimum Levenshtein (or Hamming) distance, the average random walk time increases exponentially. What this means is that populations get stuck on the peaks of these mountain ranges at very low levels of functional complexity – because neutral gap distances, or otherwise non-beneficial gap distances, are simply too wide to be crossed, this side of trillions of years of time, beyond these very low levels of functional complexity.











Drs. Pitman, Rosenhouse and Matzke
Fascinating debate on molecular evolution. I am pleased to see experts, rather than just rhetoricians such as myself, comment on scientific matters pertaining to evolution.
@ Dr. Pitman
“You mistakenly assume that human languages evolve via the same mechanism as Darwinian evolution. They do not.”
Dr. Pitman, you are the one that introduced the language metaphor to compare probabilities of genetic sequence space for new functional complexity. You are hoisting yourself on your own petard my friend!
george(Quote)
View CommentYou confuse the look of sequence space with various methods of moving about within sequence space.
All meaningful language/information systems have the same basic look of sequence spaces at various levels of functional complexity, to include an essentially uniform fairly random distribution of potentially beneficial islands within sequence space at higher levels of functional complexity. However, the mechanism by which one gets around in that space may be different. The various words that are used for similar purposes within various human languages “evolve” over time via the involvement of intelligent design (an intelligent environment if you will). The Darwinian mechanism of RM/NS does not have this option since the “environment” within which protein-based systems may evolve is not intelligent. Movement through protein-based sequence space via this method is therefore much more limited, even at the level of small individual sequences that are equivalent to most individual words in various language systems. When one starts talking about moving beyond the mere definition of small individual words, to sentences, paragraphs, and entire essays or books (i.e., higher and higher levels of functional complexity), the nature of sequence space changes exponentially with regard to the ratio of potentially beneficial vs. non-beneficial – regardless of the language/information system. With each increase in the minimum structural threshold requirement of the system (in any language/information system) the minimum likely distance between a given island and the next closest island in sequence space increases in an linear manner.
How this non-beneficial gap distance is crossed can be done with or without intelligence. It is just a matter of a significant difference in the average time required to achieve success.
If one chooses to move around in higher level sequence spaces via random mutations and function-based selection, without including intelligent manipulation of the mutations, the average random walk time required to get from one island to the next closest island within sequence space increases exponentially as the minimum gap distances increase in a linear manner. That is why the “evolution” of sentences, paragraphs, and books (and novel individual words as well) in English or Latin or Greek or Russian, etc., happens so fast – because intelligence is involved in this kind of intelligently directed “evolution”. This is not the case, however, for a mindless mechanism like RM/NS, where exponentially greater and greater amounts of time are required.
I hope this makes things a bit clearer for you…
Sean Pitman(Quote)
View Comment@ Dr. Pitman
Any possibility you could publish your paper or research, or guest lecture at the the National Institute for Mathematical and Biological Synthesis? Like Bob Helm suggested, it seems to me this is the route you are going to have to go to test your ideas and have them scrutinized by those outside the narrow creationist corridor.
george(Quote)
View Comment@ Dr. Pitman
Yes I understand the difference between the development of language vs. evolution. . I just don’t see the relevance of three dimensional molecular evolution compared to the hypothetical random combination of letters to form meaningful words, as a analogy. Thank you for your further explanation in any case
I do applaud you for bringing Drs. Rosenhouse and Matzke to the debate. This has really raised the quality of the discussion and shows your willingness to listen and debate with other experts in the field. Kudos to you 🙂
george(Quote)
View Comment3D molecular evolution is based on the proper arrangement of characters in 2D sequences, the same as in any human language system – like English or French, etc. And, the appearance of sequence space at various levels of functional complexity is also essentially the same.
Sean Pitman(Quote)
View CommentThis is not a “debate”, it’s some comments that I randomly posted on your blog, which you have fairly weirdly strung together into a single piece and then called a “debate”. That’s all you.
You still aren’t getting the difference between a “functional island” as measured by blasting a protein with multiple simultaneous mutations, and the reality, which is a web (even within a single function), the strands of which are gradually explored by a step-by-step process of various sorts of substitutions, including compensatory ones, and which would essentially never return to the starting point, or even be constrained within the region of sequences-similar-enough-to-be-identified-by-BLAST. The web covers a far, far greater area of the sequence landscape than your little island. There’s not much point in discussing more complex issues if we can’t resolve simple points like this.
Re: flagellum — the word “Pallen” does not appear in your webpage, and the homology-and-unessentiality table from that paper is not discussed.
Nick (Matzke)(Quote)
View CommentWhatever you want to call it…
I’m sorry, but I do not see how compensatory mutations 1) significantly increase the size of the islands within sequence space (as far as the absolute number of protein-based sequences in sequence space that can produce a given type of function), 2) how they create narrow paths between qualitatively different islands at higher levels of functional complexity that are significantly more likely to be traversed in a given amount of time, or 3) how they significantly narrow the non-beneficial gap distances between different islands within sequence space?
As far as I can tell, compensatory mutations are simply a way of compensating for detrimental mutations by maintaining the same basic structure and function of the system (within the overall flexibility limitations of the minimum structural threshold requirements of the system in question). I guess I just don’t see how this significantly improves the odds of finding novel islands with qualitatively novel functionality? Such has not been demonstrated anywhere in literature that I’m aware, and I personally don’t see how the odds of success could be improved by invoking compensatory mutations?
The reason for this, as far as I can tell, is that compensatory mutations are limited to producing the same basic type of structure that characterizes a particular island within sequence space. For example, “It is well known that the folding of RNA molecules into the stem-loop structure requires base pair matching in the stem part of the molecule, and mutations occurring to one segment of the stem part will disrupt the matching, and therefore, have a deleterious effect on the folding and stability of the molecule. It has been observed that mutations in the complementary segment can rescind the deleterious effect by mutating into a base pair that matches the already mutated base, thus recovering the fitness of the original molecule (Kelley et al., 2000; Wilke et al., 2003). (Link)” Of course, in this particular situation, there are very limited choices for workable compensatory mutations given the high degree of required sequence specificity of the structure.
So, as far as I can tell, this nicely illustrates my observation that compensatory mutations simply don’t produce novel structures with novel functional complexity. They simply compensate for a loss of structure/function that results from detrimental mutations by trying to get back to the original to one degree or another. This is why compensatory mutations are so constrained. Depending upon the detrimental mutation, only a limited number of compensatory mutations are possible – and most of these do not provide full functional recovery from what was lost. In other words, the original level of functionality is not entirely reproduced by most compensatory mutations. In fact, populations tend to fix compensatory mutations only when the rate of compensatory mutations exceeds the rate of reversion or back mutations by at least an order of magnitude (Levine et. al., 2000). This means, of course, that back or reversion mutations are usually the most ideal solution for resolving detrimental mutations, but are not always the first to be realized by random mutations. And, compensatory mutations are usually detrimental by themselves. That means, once a compensatory mutation occurs, it is no longer beneficial to revert the original detrimental mutation (since one would also have to revert the compensatory mutation as well). This is somewhat of a problem since since compensatory options are more common, a compensatory mutation is usually realized before a reversion mutation – up to 70% of the time (Link). However, because compensatory mutations are not generally as good as back mutations at completely restoring the original level of functionality, they are less likely to be fixed in a population – especially larger populations.
In any case, your argument that there are a number of potential compensatory mutations for most detrimental mutations (an average of 9 or so) is clearly correct. So then, doesn’t it therefore follow that these compensatory options do in fact expand the size of the island and create a net-like appearance across vast regions of sequence space? – as you originally claimed?
Consider that the overall shape of the island remains the same – with sharp peaks and steeply sloping sides. I do not see how compensatory mutational options change this basic appearance of the island? They simply make the island 10 times larger, and much more spread out, than if there were no compensatory options (as in a case of increased specificity requirements) – which isn’t really relevant given the overall size of sequence space and the ratio of beneficial vs. non-beneficial within sequence space.
For example, say that a protein sequence experiences a point mutation that happens to be detrimental. Say there are 10 potentially compensating mutational options to “fix” this protein to some useful degree, one of which is realized. Now, let’s say that this protein experiences a second detrimental mutation in a different location. Now, there are 10 more potentially compensating mutational options, one of which is realized. What happens with each additional detrimental mutation to the sequence? Is the observation of Bloom et. al., that proteins suffer an exponential decline in functionality with each additional detrimental mutation, negated by the compensatory mutation options? Not at all. The compensatory mutations simply expand the size of the island to the extent allowed by the specificity requirements of the system, but they do not make it possible for the island stretch out indefinitely over all of sequence space. The minimum structural threshold requirements simply will not allow this. The same basic structure with the same basic function and the same minimum number of required building blocks must be maintained. And, that puts a very restrictive size limit on the overall size of the island with this type of function within sequence space (size being defined by the absolute number of protein sequences that can produce a given structure with a particular type of function). In other words, the actual maximum number of protein sequences that comprise the island is very very limited.
But, you argue, compensatory mutations may allow for narrow arms or branches to extend long distances (Hamming or Levenshtein distances) within sequence space. And, this is true. However, remember that sequence space is hyperdimensional. Changing the shape of an island comprised of a limited number of grains of sand doesn’t significantly change the odds of putting it within closer range of the next closest island within sequence space. After all, the shape of the island has a random appearance that is not biased toward other surrounding islands within sequence space. Therefore, the odds of successfully locating a different island with qualitatively novel functionality remain essentially the same as far as I can tell. There is no significant change in the minimum likely gap distances between any part of the starting island, regardless of its shape, and any other island within sequence space at higher levels of functional complexity. Other islands with other types of functions still have to be found by getting off of the original island and crossing a non-selectable gap distance – and I don’t see how compensatory mutations improve these odds?
And, that, in a nutshell, is why your proposed steppingstones in your flagellar evolution pathway simply require too many non-selectable differences to get from one to the other in a reasonable amount of time.
I do discuss the homologies that you proposed in your 2003 paper, “Evolution in (Brownian) space: a model for the origin of the bacterial flagellum”.
It seems to me that they key difference you see between your 2003 and your 2006 papers is the discovery of more homologies for vital structural flagellar proteins. You write:
You see, I really don’t care if every single one of the individual protein parts within the flagellum are homologous to proteins within other systems (even though a couple of them are not currently known to be homologous to anything else). This is completely irrelevant to the plausibility of the evolution of higher level systems based on pre-existing subsystems. You see, the problem is that having all the required parts to make a new type of complex system isn’t enough. Why not? Because, these parts must be modified in very specific ways before they can work together in a new specified arrangement as parts of a different type of complex system – like a flagellar motility system. And, the number of required modifications to get the parts in your proposed pathway to work together, to any selectable advantage at a higher level of functional complexity, is simply too great to be realized this side of a practical eternity of time.
How is that? After all, is it not possible for the required parts to be perfectly homologous between different systems? Well no, it’s not. If this were the case, all kinds of very different complex systems could be produced using identical subparts. The reason why this doesn’t happen is because qualitatively different complex systems require key modifications for the otherwise homologous parts to work together in different ways. And, the great number of these required non-selectable modifications to otherwise homologous parts, the exponentially greater the average random walk time. So, by the time you’re at a level when the minimum number of required non-selectable modifications is a couple dozen or so, the average time to randomly produce all of these required modifications, which cannot be guided by natural selection, is trillions upon trillions of years. And, I fail to see how compensatory mutations help to solve this problem? As far as I can tell, they do nothing to solve this problem for the ToE.
In short, homologies simply don’t cut it because it isn’t the similarities that are important, but the number of required non-selectable modifications that completely kills off evolutionary potential, in an exponential manner, beyond very low levels of functional complexity.
Sean Pitman(Quote)
View CommentI find it quite amusing how we argue evolution with a straight face and are so hypothetical, philosophical, and imaginary. It’s not what could be or what should be. It’s actually what is! When we take the ‘what is’ and run it backwards to the earliest beginnings we find that there is no difference between what is and what was. The evolutionary concept of ‘evolving’ is very hard to come by. We do not see it. And what we see is in itself a complete whole and not an evolutionary misfit. For the religion of evolution to survive it has to exercises humongous faith and story telling but without any specimen and its generation before them. For creationists there is only one model and that is the Genesis account. And by the Genesis account I mean a literal acceptance of Genesis and all support passages through out the Scriptures. I do not refer to ‘other’ creation accounts that would neuter the Genesis narration. These are akin to the varied evolutionists’ accounts of origins. The ‘debate’ was like watching two individuals debate the origin of a motor car parked in front of them. Each had his imagination, philosophy, and supposition. Except if the car could talk it would say, first, you both were not there and so are badly off track. Secondly, it would say, I was made by someone with intelligence, humor, and skill. Of course for the evolutionist to say that would give the game away and their religion would become extinct! One day it will, believe it or not!
Ron Henderson(Quote)
View Comment@ Ron
“The ‘debate’ was like watching two individuals debate the origin of a motor car parked in front of them. Each had his imagination, philosophy, and supposition. Except if the car could talk it would say, first, you both were not there and so are badly off track.”
Interesting analogy. Presumably one of your hypothetical debaters is a creationist, Dr. Pitman? Are you saying that Dr. Pitman is off track because he is a YLC and I presume you might be a YEC? Please elaborate in order that the readers can understand who the individuals are in your analogy.
george(Quote)
View CommentPingback: Homologies, Phylogenies, Sequence Space and the Theory of Evolution | Educate Truth
This is not a “debate”, it’s some comments that I randomly posted on your blog, which you have fairly weirdly strung together into a single piece and then called a “debate”. That’s all you.
You still aren’t getting the difference between a “functional island” as measured by blasting a protein with multiple simultaneous mutations, and the reality, which is a web (even within a single function), the strands of which are gradually explored by a step-by-step process of various sorts of substitutions, including compensatory ones, and which would essentially never return to the starting point, or even be constrained within the region of sequences-similar-enough-to-be-identified-by-BLAST. The web covers a far, far greater area of the sequence landscape than your little island. There’s not much point in discussing more complex issues if we can’t resolve simple points like this.
Re: flagellum — the word “Pallen” does not appear in your webpage, and the homology-and-unessentiality table from that paper is not discussed.
Nick (Matzke)(Quote)
View CommentWhatever you want to call it…
I’m sorry, but I do not see how compensatory mutations 1) significantly increase the size of the islands within sequence space (as far as the absolute number of protein-based sequences in sequence space that can produce a given type of function), 2) how they create narrow paths between qualitatively different islands at higher levels of functional complexity that are significantly more likely to be traversed in a given amount of time, or 3) how they significantly narrow the non-beneficial gap distances between different islands within sequence space?
As far as I can tell, compensatory mutations are simply a way of compensating for detrimental mutations by maintaining the same basic structure and function of the system (within the overall flexibility limitations of the minimum structural threshold requirements of the system in question). I guess I just don’t see how this significantly improves the odds of finding novel islands with qualitatively novel functionality? Such has not been demonstrated anywhere in literature that I’m aware, and I personally don’t see how the odds of success could be improved by invoking compensatory mutations?
The reason for this, as far as I can tell, is that compensatory mutations are limited to producing the same basic type of structure that characterizes a particular island within sequence space. For example, “It is well known that the folding of RNA molecules into the stem-loop structure requires base pair matching in the stem part of the molecule, and mutations occurring to one segment of the stem part will disrupt the matching, and therefore, have a deleterious effect on the folding and stability of the molecule. It has been observed that mutations in the complementary segment can rescind the deleterious effect by mutating into a base pair that matches the already mutated base, thus recovering the fitness of the original molecule (Kelley et al., 2000; Wilke et al., 2003). (Link)” Of course, in this particular situation, there are very limited choices for workable compensatory mutations given the high degree of required sequence specificity of the structure.
So, as far as I can tell, this nicely illustrates my observation that compensatory mutations simply don’t produce novel structures with novel functional complexity. They simply compensate for a loss of structure/function that results from detrimental mutations by trying to get back to the original to one degree or another. This is why compensatory mutations are so constrained. Depending upon the detrimental mutation, only a limited number of compensatory mutations are possible – and most of these do not provide full functional recovery from what was lost. In other words, the original level of functionality is not entirely reproduced by most compensatory mutations. In fact, populations tend to fix compensatory mutations only when the rate of compensatory mutations exceeds the rate of reversion or back mutations by at least an order of magnitude (Levine et. al., 2000). This means, of course, that back or reversion mutations are usually the most ideal solution for resolving detrimental mutations, but are not always the first to be realized by random mutations. And, compensatory mutations are usually detrimental by themselves. That means, once a compensatory mutation occurs, it is no longer beneficial to revert the original detrimental mutation (since one would also have to revert the compensatory mutation as well). This is somewhat of a problem since since compensatory options are more common, a compensatory mutation is usually realized before a reversion mutation – up to 70% of the time (Link). However, because compensatory mutations are not generally as good as back mutations at completely restoring the original level of functionality, they are less likely to be fixed in a population – especially larger populations.
In any case, your argument that there are a number of potential compensatory mutations for most detrimental mutations (an average of 9 or so) is clearly correct. So then, doesn’t it therefore follow that these compensatory options do in fact expand the size of the island and create a net-like appearance across vast regions of sequence space? – as you originally claimed?
Consider that the overall shape of the island remains the same – with sharp peaks and steeply sloping sides. I do not see how compensatory mutational options change this basic appearance of the island? They simply make the island 10 times larger, and much more spread out, than if there were no compensatory options (as in a case of increased specificity requirements) – which isn’t really relevant given the overall size of sequence space and the ratio of beneficial vs. non-beneficial within sequence space.
For example, say that a protein sequence experiences a point mutation that happens to be detrimental. Say there are 10 potentially compensating mutational options to “fix” this protein to some useful degree, one of which is realized. Now, let’s say that this protein experiences a second detrimental mutation in a different location. Now, there are 10 more potentially compensating mutational options, one of which is realized. What happens with each additional detrimental mutation to the sequence? Is the observation of Bloom et. al., that proteins suffer an exponential decline in functionality with each additional detrimental mutation, negated by the compensatory mutation options? Not at all. The compensatory mutations simply expand the size of the island to the extent allowed by the specificity requirements of the system, but they do not make it possible for the island stretch out indefinitely over all of sequence space. The minimum structural threshold requirements simply will not allow this. The same basic structure with the same basic function and the same minimum number of required building blocks must be maintained. And, that puts a very restrictive size limit on the overall size of the island with this type of function within sequence space (size being defined by the absolute number of protein sequences that can produce a given structure with a particular type of function). In other words, the actual maximum number of protein sequences that comprise the island is very very limited.
But, you argue, compensatory mutations may allow for narrow arms or branches to extend long distances (Hamming or Levenshtein distances) within sequence space. And, this is true. However, remember that sequence space is hyperdimensional. Changing the shape of an island comprised of a limited number of grains of sand doesn’t significantly change the odds of putting it within closer range of the next closest island within sequence space. After all, the shape of the island has a random appearance that is not biased toward other surrounding islands within sequence space. Therefore, the odds of successfully locating a different island with qualitatively novel functionality remain essentially the same as far as I can tell. There is no significant change in the minimum likely gap distances between any part of the starting island, regardless of its shape, and any other island within sequence space at higher levels of functional complexity. Other islands with other types of functions still have to be found by getting off of the original island and crossing a non-selectable gap distance – and I don’t see how compensatory mutations improve these odds?
And, that, in a nutshell, is why your proposed steppingstones in your flagellar evolution pathway simply require too many non-selectable differences to get from one to the other in a reasonable amount of time.
I do discuss the homologies that you proposed in your 2003 paper, “Evolution in (Brownian) space: a model for the origin of the bacterial flagellum”.
It seems to me that they key difference you see between your 2003 and your 2006 papers is the discovery of more homologies for vital structural flagellar proteins. You write:
You see, I really don’t care if every single one of the individual protein parts within the flagellum are homologous to proteins within other systems (even though a couple of them are not currently known to be homologous to anything else). This is completely irrelevant to the plausibility of the evolution of higher level systems based on pre-existing subsystems. You see, the problem is that having all the required parts to make a new type of complex system isn’t enough. Why not? Because, these parts must be modified in very specific ways before they can work together in a new specified arrangement as parts of a different type of complex system – like a flagellar motility system. And, the number of required modifications to get the parts in your proposed pathway to work together, to any selectable advantage at a higher level of functional complexity, is simply too great to be realized this side of a practical eternity of time.
How is that? After all, is it not possible for the required parts to be perfectly homologous between different systems? Well no, it’s not. If this were the case, all kinds of very different complex systems could be produced using identical subparts. The reason why this doesn’t happen is because qualitatively different complex systems require key modifications for the otherwise homologous parts to work together in different ways. And, the great number of these required non-selectable modifications to otherwise homologous parts, the exponentially greater the average random walk time. So, by the time you’re at a level when the minimum number of required non-selectable modifications is a couple dozen or so, the average time to randomly produce all of these required modifications, which cannot be guided by natural selection, is trillions upon trillions of years. And, I fail to see how compensatory mutations help to solve this problem? As far as I can tell, they do nothing to solve this problem for the ToE.
In short, homologies simply don’t cut it because it isn’t the similarities that are important, but the number of required non-selectable modifications that completely kills off evolutionary potential, in an exponential manner, beyond very low levels of functional complexity.
Sean Pitman(Quote)
View Comment@ Ron
“The ‘debate’ was like watching two individuals debate the origin of a motor car parked in front of them. Each had his imagination, philosophy, and supposition. Except if the car could talk it would say, first, you both were not there and so are badly off track.”
Interesting analogy. Presumably one of your hypothetical debaters is a creationist, Dr. Pitman? Are you saying that Dr. Pitman is off track because he is a YLC and I presume you might be a YEC? Please elaborate in order that the readers can understand who the individuals are in your analogy.
george(Quote)
View Comment@ Dr. Pitman
Any possibility you could publish your paper or research, or guest lecture at the the National Institute for Mathematical and Biological Synthesis? Like Bob Helm suggested, it seems to me this is the route you are going to have to go to test your ideas and have them scrutinized by those outside the narrow creationist corridor.
george(Quote)
View Comment@ Dr. Pitman
Yes I understand the difference between the development of language vs. evolution. . I just don’t see the relevance of three dimensional molecular evolution compared to the hypothetical random combination of letters to form meaningful words, as a analogy. Thank you for your further explanation in any case
I do applaud you for bringing Drs. Rosenhouse and Matzke to the debate. This has really raised the quality of the discussion and shows your willingness to listen and debate with other experts in the field. Kudos to you 🙂
george(Quote)
View Comment3D molecular evolution is based on the proper arrangement of characters in 2D sequences, the same as in any human language system – like English or French, etc. And, the appearance of sequence space at various levels of functional complexity is also essentially the same.
Sean Pitman(Quote)
View CommentDrs. Pitman, Rosenhouse and Matzke
Fascinating debate on molecular evolution. I am pleased to see experts, rather than just rhetoricians such as myself, comment on scientific matters pertaining to evolution.
@ Dr. Pitman
“You mistakenly assume that human languages evolve via the same mechanism as Darwinian evolution. They do not.”
Dr. Pitman, you are the one that introduced the language metaphor to compare probabilities of genetic sequence space for new functional complexity. You are hoisting yourself on your own petard my friend!
george(Quote)
View CommentYou confuse the look of sequence space with various methods of moving about within sequence space.
All meaningful language/information systems have the same basic look of sequence spaces at various levels of functional complexity, to include an essentially uniform fairly random distribution of potentially beneficial islands within sequence space at higher levels of functional complexity. However, the mechanism by which one gets around in that space may be different. The various words that are used for similar purposes within various human languages “evolve” over time via the involvement of intelligent design (an intelligent environment if you will). The Darwinian mechanism of RM/NS does not have this option since the “environment” within which protein-based systems may evolve is not intelligent. Movement through protein-based sequence space via this method is therefore much more limited, even at the level of small individual sequences that are equivalent to most individual words in various language systems. When one starts talking about moving beyond the mere definition of small individual words, to sentences, paragraphs, and entire essays or books (i.e., higher and higher levels of functional complexity), the nature of sequence space changes exponentially with regard to the ratio of potentially beneficial vs. non-beneficial – regardless of the language/information system. With each increase in the minimum structural threshold requirement of the system (in any language/information system) the minimum likely distance between a given island and the next closest island in sequence space increases in an linear manner.
How this non-beneficial gap distance is crossed can be done with or without intelligence. It is just a matter of a significant difference in the average time required to achieve success.
If one chooses to move around in higher level sequence spaces via random mutations and function-based selection, without including intelligent manipulation of the mutations, the average random walk time required to get from one island to the next closest island within sequence space increases exponentially as the minimum gap distances increase in a linear manner. That is why the “evolution” of sentences, paragraphs, and books (and novel individual words as well) in English or Latin or Greek or Russian, etc., happens so fast – because intelligence is involved in this kind of intelligently directed “evolution”. This is not the case, however, for a mindless mechanism like RM/NS, where exponentially greater and greater amounts of time are required.
I hope this makes things a bit clearer for you…
Sean Pitman(Quote)
View CommentI find it quite amusing how we argue evolution with a straight face and are so hypothetical, philosophical, and imaginary. It’s not what could be or what should be. It’s actually what is! When we take the ‘what is’ and run it backwards to the earliest beginnings we find that there is no difference between what is and what was. The evolutionary concept of ‘evolving’ is very hard to come by. We do not see it. And what we see is in itself a complete whole and not an evolutionary misfit. For the religion of evolution to survive it has to exercises humongous faith and story telling but without any specimen and its generation before them. For creationists there is only one model and that is the Genesis account. And by the Genesis account I mean a literal acceptance of Genesis and all support passages through out the Scriptures. I do not refer to ‘other’ creation accounts that would neuter the Genesis narration. These are akin to the varied evolutionists’ accounts of origins. The ‘debate’ was like watching two individuals debate the origin of a motor car parked in front of them. Each had his imagination, philosophy, and supposition. Except if the car could talk it would say, first, you both were not there and so are badly off track. Secondly, it would say, I was made by someone with intelligence, humor, and skill. Of course for the evolutionist to say that would give the game away and their religion would become extinct! One day it will, believe it or not!
Ron Henderson(Quote)
View Comment