 How is plagiarism detected? Let’s say a student claims to have written an original paper, but his teacher discovers that much of it appears to be identical, save for few words here and there, and a few paragraph modifications, to a paper she discovered on the internet. Would this not be excellent evidence that the student’s paper is not original work? – that the student did in fact “borrow” the work from someone else? – that the paper in question was derived from another source?
How is plagiarism detected? Let’s say a student claims to have written an original paper, but his teacher discovers that much of it appears to be identical, save for few words here and there, and a few paragraph modifications, to a paper she discovered on the internet. Would this not be excellent evidence that the student’s paper is not original work? – that the student did in fact “borrow” the work from someone else? – that the paper in question was derived from another source?
Scientists come to the very some conclusions when it comes to the study of biology. Various anatomic and genetic similarities are judged to have been derived from a common source or origin. For example, most of the gene comparisons between humans and apes are nearly identical. And, even a comparison between humans and bananas produces ~50% genetic similarity for various gene comparisons (Link). In fact, all living things share so many features, to include the same basic genetic code and basic building blocks (for DNA, RNA, and proteins) that it seems certain that all life on this planet did in fact have a common origin of some kind. The question, of course, is what common origin?
Most scientists today believe that the common origin of all life on this planet can best be explained by the modern view of Darwinian Evolution where life on this planet began in some primordial pond where the basic building blocks self-assembled to produce the first living, self-replicating, single celled organism. From this humble beginning, random genetic mutations and natural selection (RM/NS) took over and transformed this first living thing, over a billion years or so, into all the diversity of life that we see today.
However, there are a few who question this popular story of common descent via the evolutionary mechanism of random mutations and natural selection (RM/NS). Although a distinct minority, both creationists and those who wish to promote various concepts of intelligent design argue that the Darwinian mechanism isn’t capable of explaining the fantastic diversity of life at such high levels of functional complexity that currently exists on this planet. Even those IDists who believe in common descent of some kind over vast periods of time argue that some very intelligent and very powerful mind, even a God or a God-like mind, must have been involved with the creation of life and its diversity on this planet.
Table of Contents
The Tree of Life
How then does one tell which theory is most likely true? Is life and its diversity on this planet the result of a mindless natural mechanism or deliberate intelligent design? What should one expect given the truth of either theory?
 Evolutionary biologists have ready answer. They point to something known as the “Tree of Life” where all living things can be classified along tree-like branches according to predictable patterns of similarities and differences. And, the resulting pattern of similarities and differences looks very much like a tree with almost all living things neatly arranged in a “nested hierarchical pattern” (NHP) of organization – exactly what would be expected from a mechanism that produced very gradual changes over very long periods of time in various gradually diverging populations. It is this predictable order of living things that allows for the science of taxonomy, or the orderly classification of living things according to their morphologic and/or genetic similarities and differences – a science that began with the work of Carolus Linnaeus, the father of taxonomy and concepts like: Kingdom, Phylum, Class, Order, Family, Genus, and Species.
Evolutionary biologists have ready answer. They point to something known as the “Tree of Life” where all living things can be classified along tree-like branches according to predictable patterns of similarities and differences. And, the resulting pattern of similarities and differences looks very much like a tree with almost all living things neatly arranged in a “nested hierarchical pattern” (NHP) of organization – exactly what would be expected from a mechanism that produced very gradual changes over very long periods of time in various gradually diverging populations. It is this predictable order of living things that allows for the science of taxonomy, or the orderly classification of living things according to their morphologic and/or genetic similarities and differences – a science that began with the work of Carolus Linnaeus, the father of taxonomy and concepts like: Kingdom, Phylum, Class, Order, Family, Genus, and Species.
The question is then asked, why appeal to some God or intelligent designer who tinkers, undetectably, with life on our planet over vast periods of time when there is a perfectly good naturalistic explanation for how the patterns and relationships of living things we observe living today, and within the fossil record, came to be?
Well, the question isn’t if a NHP can be produced by random mutations and natural selection. Clearly, such a pattern of tree-like branching similarities and differences can be produced over time by RM/NS. So, what’s the problem? – besides wishful thinking on the part of Bible-thumping creationists and those who favor intelligent design? The problem is that the mechanism of RM/NS doesn’t seem to be able to explain all of the features observed within living things.
How is that? What is it that RM/NS cannot readily explain given a billion or so years of time?
Levels of Functional Complexity
RM/NS can explained shared similarities and certain kinds of differences, in a NHP, but RM/NS cannot readily explain functional differences beyond very low levels of functional complexity. It’s not the similarities, but the functional differences, that strike at the heart of the theory. This is the entire problem with the claims of modern evolutionists – their mechanism doesn’t appear to be up to the job required of it for the theory to be true. There is a very clear limitation to evolutionary progress beyond very low levels of functional complexity this side of a practical eternity of time.
But what do I mean by “levels of functional complexity”? Has this concept even been defined in science?
The concept of a level of functional complexity has been defined in scientific literature by those like Hazen et. al. (2007), among others.8 And, it is a pretty straightforward intuitively-obvious definition. In short, a level of functional complexity is defined by the minimum number of parts or basic building blocks required to produce a particular type of system or a meaningful/functional sequence with a qualitatively unique function – as well as how precisely the parts must be arranged before a useful level of meaning/function can be realized (also known as the specificity requirement).
For example, consider the following sequences (from the perspective of the English language system):
- AAAAAAAAAAAAAAAAAAAAA – Specified, but not complex
- AGVBRVSO LPNMQRZ KKLTPX – Complex, but not specified (i.e., a randomly generated sequence)
- Methinks it is like a weasel. – Complex and specified (and functional/meaningful)
- Weasel – Complex and specified, but on a lower level of functional complexity
The Increasing Non-beneficial Gap Problem
As it turns out, with each increase in the minimum size and/or specificity requirement of a system (or any informational language system, such as English, French, Russian, Morse Code, computer codes, DNA, proteins, etc.), the average number of mutational changes that are required to get from one such system to the next closest system (at the same level of functional complexity or higher) increases in a linear manner. And, with each linear increase in minimum number of modifications required to find something functionally new, the average number of random mutations or modifications required to achieve success increases exponentially. This results in an exponential stalling-out effect of evolutionary progress at very low levels of functional complexity.
For example, consider the evolutionary sequence:
- CAT-HAT-BAT-BAD-BID-DID-DIG-DOG
Is this not a clear evolutionary sequence where every single character change results in a new meaningful word? What then is the problem for the evolutionary algorithm of random mutations and function-based selection?
Consider that it is relatively easy to move around between three-letter words because meaningful three-letter words are so close together in “sequence space” (a space that contains all possible arrangement of characters of a certain length). In fact, the ratio of meaningful vs. meaningless three-letter sequences in the English Scrabble Dictionary is about 1 in 18. However, what happens when the minimum size requirement is increased to 7-character sequences comprised of one or more “words”? Well, 7-character sequences are not so closely spaced on average because the ratio of meaningful vs. meaningless decreases, exponentially, to about 1 in 250,000 at this level of functional complexity (within the English language system). So, the average time to success for the evolutionary algorithm must also increase exponentially with each step up the ladder of functional complexity.
 The very same thing happens in biology with DNA and proteins. For example, direct experimentally-determined degrees of protein sequence flexibility by those like Durston, Sauer, Olsen, Bowie, Axe, and others show that the vast majority of possible protein sequences, of a given size, are unstable and cannot even be maintained within living things, much less produce any beneficial effect.1-5 Consider a fairly small 150aa protein, for instance. The total number of possible sequences of 150aa in length is 20150, or 1e195 sequences. This is an enormous number of sequences. After all, the total number of atoms in the visible universe is only about 1e80. So, out of this total number, how many of these protein sequences could actually produce a stable protein? Experimental studies by those like Thirumalai (2000) and Axe (2011) show that only about 1 in 1074 sequences of 150aa in size are even capable of forming stable protein folds.6-7 As it turns out, this ratio decreases, exponentially, with each linear increase in the minimum size requirement of the protein-based system. In other words, as sequence space grows by 20N, the number of stable protein structures only scales by the natural log of N.6 Now, consider that protein stability isn’t the only thing that makes a protein beneficial. Requiring that a protein not only be stable, but beneficial as well before natural selection can preferentially maintain it reduces the ratio of such proteins in 150aa sequence space to about 1 in 1077. And, with each step up the ladder of functional complexity, this ratio gets exponentially worse and worse.
The very same thing happens in biology with DNA and proteins. For example, direct experimentally-determined degrees of protein sequence flexibility by those like Durston, Sauer, Olsen, Bowie, Axe, and others show that the vast majority of possible protein sequences, of a given size, are unstable and cannot even be maintained within living things, much less produce any beneficial effect.1-5 Consider a fairly small 150aa protein, for instance. The total number of possible sequences of 150aa in length is 20150, or 1e195 sequences. This is an enormous number of sequences. After all, the total number of atoms in the visible universe is only about 1e80. So, out of this total number, how many of these protein sequences could actually produce a stable protein? Experimental studies by those like Thirumalai (2000) and Axe (2011) show that only about 1 in 1074 sequences of 150aa in size are even capable of forming stable protein folds.6-7 As it turns out, this ratio decreases, exponentially, with each linear increase in the minimum size requirement of the protein-based system. In other words, as sequence space grows by 20N, the number of stable protein structures only scales by the natural log of N.6 Now, consider that protein stability isn’t the only thing that makes a protein beneficial. Requiring that a protein not only be stable, but beneficial as well before natural selection can preferentially maintain it reduces the ratio of such proteins in 150aa sequence space to about 1 in 1077. And, with each step up the ladder of functional complexity, this ratio gets exponentially worse and worse.
What this means is that when one starts considering protein-based systems that require more than 1000aa with an average degree of specificity, the minimum likely distance between any such system and the next closest system in sequence space is well over 150 non-selectable mutational changes. In other words, it would take well over 150 modifications to the protein-based system to get it to produce a qualitatively new kind of function at the same level of functional complexity or higher.9 How long would 150 non-selectable mutations take to achieve within a large population?
Well, consider that the number of all the bacteria on Earth is about 1e30 and the total number of living things that are thought to have ever lived on Earth is less than 1e40.7 The size of the non-selectable search space is about 20150 = 1e195 sequences between one steppingstone and the next closest stepping stone in 1000aa sequence space. Assuming one random mutation in every single 1000aa sequence in every one of our organisms every 30 minutes (with no detrimental mutations), it would take more than 1e140 years to achieve success on average – a practical eternity of time.
 So, what are some examples of biological systems that require more than 1000 averagely specified amino acid building blocks? Well, there are numerous sub-cellular mechanical machines that require well over 1000 specifically arranged amino acid residue positions in order to produce a particular type of function within the cell. The famous rotary bacterial flagellum is one good example. Such a flagellar motility system appears to require a minimum of at least 23 structural proteins to be specifically arranged relative to each other in 3D space.10 These proteins, of course, require a total of over 5,000aa to be specifically arranged in 3D space as well. And, this is only a small subcellular machine. All living things are vastly more complex than such a small subcellular machine – none of which have ever been shown to evolve in the lab nor has it ever been shown, by anyone, how the non-selectable gap distances are actually small enough to be crossed by random mutations in a reasonable amount of time. The fairly well-known evolutionary biologist Nick Matzke, in particular, has tried valiantly to show how various pre-existing homologous parts within other systems of function can sequentially fuse together over time to produce various selectable steppingstones in a pathway toward flagellar evolution.9,10 However, each one of Matzke’s proposed steppingstones is far too far away from the next steppingstone for the resulting gap distances to be crossed in a reasonable amount of time.
So, what are some examples of biological systems that require more than 1000 averagely specified amino acid building blocks? Well, there are numerous sub-cellular mechanical machines that require well over 1000 specifically arranged amino acid residue positions in order to produce a particular type of function within the cell. The famous rotary bacterial flagellum is one good example. Such a flagellar motility system appears to require a minimum of at least 23 structural proteins to be specifically arranged relative to each other in 3D space.10 These proteins, of course, require a total of over 5,000aa to be specifically arranged in 3D space as well. And, this is only a small subcellular machine. All living things are vastly more complex than such a small subcellular machine – none of which have ever been shown to evolve in the lab nor has it ever been shown, by anyone, how the non-selectable gap distances are actually small enough to be crossed by random mutations in a reasonable amount of time. The fairly well-known evolutionary biologist Nick Matzke, in particular, has tried valiantly to show how various pre-existing homologous parts within other systems of function can sequentially fuse together over time to produce various selectable steppingstones in a pathway toward flagellar evolution.9,10 However, each one of Matzke’s proposed steppingstones is far too far away from the next steppingstone for the resulting gap distances to be crossed in a reasonable amount of time.
Flexible Proteins
Matzke, and other evolutionary biologists like him, argue that not only can different proteins, or protein domains, fuse together to form more complex systems, but that the protein sequences themselves are far more flexible than other language/information systems.
Proteins are much more flexible than, say, English. It is commonplace to find protein families where 50% or even 80% of the amino acids have changed, yet the structure and function remain the same. – Nick Matzke
However, consider the following sentence:
Waht I ma ytring ot asy heer si htat nEgilsh is airfly exflbie oot.
You see, a sequence of letters can be pretty flexible in the context of an English-speaking environment and still get the intended idea across. The same is true for protein sequences. Most of the amino acid characters in a protein sequence can be changed, one at a time, without a complete loss of original function. And, if carefully selected, multiple amino acid positions can be changed at the same time, 50% or even 80% on occasion, without a complete loss of original function. This is especially true of the central hydrophobic regions of proteins, “a high fraction” of which can be mutated, at the same time, without a complete loss of original function.7 However, the exterior amino acids of a protein generally require a higher level of specificity and cannot be so easily mutated, even among the most similar amino acid alternatives, without a significant loss of function.7
Of course, multiple completely random mutations that hit a protein at the same time do tend to result in an exponential decline in functionality.13 However, carefully selected mutations can “compensate” for each other, and result in greater diversity of protein sequences without a complete loss in function.
What this means, then, is that although there is a fair degree of flexibility for most types of protein-based systems, there is also a fair degree of specificity required as well, beyond which the function in question will cease to exist at a selectable level in a given environment. In other words, an average protein will be able to experience an average of 2.2 amino acid substitutions, per amino acid position in the sequence, without a complete loss of function.12 Considering that there are 20 possible amino acid options, the potential for an average of just 2.2 options per position in a protein sequence is still a fairly sizable restraint on protein flexibility. So, at this point it seems quite clear that the argument that up to 80% of a protein sequence can be changed without a significant loss of function simply doesn’t reflect the true limitations on sequence flexibility for most protein-based systems. This is the reason why, as one considers protein-based systems that require a larger and larger number of amino acids to produce a given function, the ratio of stable/functional proteins within these larger sequences spaces still drops off exponentially.
 Of course, at lower levels the ratio of beneficial vs. non-beneficial is still relatively high. For example, approximately 1 in 1011 protein sequences of 80aa in length will show ATP binding activity.11 Remember, however, that ATP binding is a very simple function that doesn’t involve catalyzing an enzymatic transformation, etc. For a step up the ladder to something requiring a bit more sequence specificity, consider that the enzymatic function of corismate mutase (a metabolic enzyme necessary for amino acid biosynthesis) can be realized in only 1 out of 1024 random protein sequences that are 93aa in size – a difference of 13 orders of magnitude. Sure, the total number of sequences in 93aa sequence space that could produce the corismate mutase function is quite large at 1e96 sequences. However, consider that for each and every one of these 1e96 sequences there are 1e24 sequences that cannot produce this particular type of function. What this means, then, is that although the corismate mutase island may seem extremely large from one perspective, it is the tiniest grain of sand from the perspective of the hyperdimentional sequence space that contains it. And, by the time one starts considering 150aa sequence space, the ratio of stable protein sequences (not even functional protein sequences) is only 1 in 1074 sequences.7
Of course, at lower levels the ratio of beneficial vs. non-beneficial is still relatively high. For example, approximately 1 in 1011 protein sequences of 80aa in length will show ATP binding activity.11 Remember, however, that ATP binding is a very simple function that doesn’t involve catalyzing an enzymatic transformation, etc. For a step up the ladder to something requiring a bit more sequence specificity, consider that the enzymatic function of corismate mutase (a metabolic enzyme necessary for amino acid biosynthesis) can be realized in only 1 out of 1024 random protein sequences that are 93aa in size – a difference of 13 orders of magnitude. Sure, the total number of sequences in 93aa sequence space that could produce the corismate mutase function is quite large at 1e96 sequences. However, consider that for each and every one of these 1e96 sequences there are 1e24 sequences that cannot produce this particular type of function. What this means, then, is that although the corismate mutase island may seem extremely large from one perspective, it is the tiniest grain of sand from the perspective of the hyperdimentional sequence space that contains it. And, by the time one starts considering 150aa sequence space, the ratio of stable protein sequences (not even functional protein sequences) is only 1 in 1074 sequences.7
It is quite clear, yet again, that with each step up the ladder of functional complexity, the ratio of potentially beneficial vs. non-beneficial decreases exponentially. How then can evolutionists still believe that their Darwinian mechanism is remotely up the the job beyond the lowest levels of functional complexity that are found within every living thing on this planet?
Complexity from the Fusion of Smaller Parts
Well, there are various attempts to explain how such enormous odds against the evolutionary mechanism can be overcome. For example, there is the very popular argument that pre-existing proteins, protein domains, and protein-based systems, which are clearly independently stable and functional on their own, can be fused together to form new higher level systems. Such a prediction seems to make sense at first approximation since it seems to overcome the problem of having to cross vast unstable unfoldable regions within protein sequence space. This theory also predicts that higher level systems, such as the bacterial flagellar motility system, will therefore be comprised of protein subparts and subsystems that can also be found doing other jobs within the cell or within other bacteria. And, this prediction has been very successful. After all, nearly all of the 23 proteins that are vital for the bacterial flagellum are homologous to proteins within other systems of function.10 Is this not therefore a clear vindication of the theory?
Not quite. The problem is that getting the homologous proteins to link up in the precise manner required for the higher-level system to be realized requires that each homologous protein be modified in very precise ways. Otherwise, they simply will not arrange themselves properly in 3D space or have exactly the proper features needed to achieve the new higher-level system. And, with each step up the ladder of functional complexity, the number of required, non-selectable, modifications needed to achieve success increases in a linear manner. And, with each increase in the number of required modifications, none of which are selectable by natural selection, the average time to success increases exponentially.9
 The argument, though, is that such flexibility allows for random mutations and function-based selection to much more easily find new sequences in sequence space that have novel functionality. How so, if sequence space is so very sparsely populated by potentially beneficial sequences with novel functionality? Because, if a protein-based system can achieve upwards of 80% flexibility without a significant loss of function, pretty much the entire Hamming distance across sequence space can be traversed by one single “island cluster” of sequences. Remember, however, that protein sequence space isn’t based on just two or even three dimensions, but on hundreds and thousands of dimensions – depending upon the length of the protein sequence. In other words protein sequence space is hyperdimensional (with one extra dimension for every additional amino acid residue in the sequence). This means that what seems like a large island from the perspective of two dimensions is really a very very tiny island from the perspective of hundreds or thousands of dimensions (kind of like widely separated balloons floating in a room looking like they’re really close together, or even overlapping each other, when looking at their shadow on one of the walls in the room).
The argument, though, is that such flexibility allows for random mutations and function-based selection to much more easily find new sequences in sequence space that have novel functionality. How so, if sequence space is so very sparsely populated by potentially beneficial sequences with novel functionality? Because, if a protein-based system can achieve upwards of 80% flexibility without a significant loss of function, pretty much the entire Hamming distance across sequence space can be traversed by one single “island cluster” of sequences. Remember, however, that protein sequence space isn’t based on just two or even three dimensions, but on hundreds and thousands of dimensions – depending upon the length of the protein sequence. In other words protein sequence space is hyperdimensional (with one extra dimension for every additional amino acid residue in the sequence). This means that what seems like a large island from the perspective of two dimensions is really a very very tiny island from the perspective of hundreds or thousands of dimensions (kind of like widely separated balloons floating in a room looking like they’re really close together, or even overlapping each other, when looking at their shadow on one of the walls in the room).
But, what about the possibility of fusing domains into larger proteins? Or, what about fusing pre-existing proteins into larger multiprotein systems? Doesn’t this avoid the problem of crossing vast unstable regions of sequence space? After all, proteins are comprised of sub-units called “domains”, which can act independently or in concert with other domains to produce novel functions. In this way, protein domains are equivalent to words in human language systems. And, as words can be combined in various different ways to produce different meanings, so protein domain “words” can also be combined in different ways to produce different types of protein-based functions within living things. After all, so far, more than 1200 unique protein domains have been discovered (Link). And, with 1200 words in your language, you can produce a lot of different sentences, paragraphs, and entire books!
While this may seem like a winning idea at first approximation, there are a couple major problems with this theory. The first problem is that, just like words in the English language system, there are numerous ways in which proteins or protein domains could combine with each other, the vast majority of which would not be beneficial (again, the problem of the rarity of beneficial arrangements of “letters” or “words” in sequence space).
The other problem is that protein domains are not like Legos that can be stuck together at will without the need for appropriate modifications. A domain that worked well in one protein will not work at all in another protein – even if the other protein has very similar structure and the same type of function – as illustrated below and described by Ann Gauger in her 2012 article (Link).
In short, in order for domains or proteins that work within one system to work as parts of a different system, even if they happen to get stuck together in the proper order (which would be quite a trick all by itself), they must be appropriately modified so that they can work together in novel ways to form novel structures and produce qualitatively novel functions at higher and higher levels of functional complexity. How are these required modifications achieved? – modifications that are not sequentially selectable by a function-based system of selection? If they are to be achieved by random mutations, they must all be achieved before the newly evolved system will actually work to a selectable level of functionality. And remember, the number of these required modifications increases with each step up the ladder of functional complexity.
It seems then that homologous proteins and protein-based systems are not homologous enough to remove the problem of the linearly increasing gap distances between selectable islands within sequence space with each step up the ladder of functional complexity.
 Of course, there are other arguments, each of which have exactly the same fundamental problem explaining evolution at higher levels of functional complexity. For example, consider the frustration of Stephen Meyer as he makes a similar observation in his latest book “Darwin’s Doubt.”
Of course, there are other arguments, each of which have exactly the same fundamental problem explaining evolution at higher levels of functional complexity. For example, consider the frustration of Stephen Meyer as he makes a similar observation in his latest book “Darwin’s Doubt.”
“These scenarios invoke various kinds of mutations – duplication events, exon shuffling, retropositioning, lateral gene transfer, and subsequent point mutations – as well as the activity of natural selection. The evolutionary biologists conducting these studies postulate that modern genes arose as the result of these various mutational processes – processes that they envision as having shaped genes during a long evolutionary history. Since the information in modern genes is presumably different form the information in the hypothetical ancestor genes, they regard the mutation mechanisms that are allegedly responsible for these differences as the explanation for the origin of genetic information.
Upon closer examination, however, none of these papers demonstrate how mutations and natural selection could find truly novel genes or proteins in sequence space in the first place; nor do they how that it is reasonably provable (or plausible) that these mechanisms would to so in the time available. These papers assume the existence of significant amounts of preexisting genetic information (indeed, many whole and unique genes) and then suggest various mechanisms that might have slightly altered or fused these genes together into larger composites At best, these scenarios “trace” the history of preexisting genes, rather than explain the origin of the original genes themselves.
This kind of scenario building can suggest potentially fruitful avenues of research. But an obvious error comes in mistaking a hypothetical scenario for either a demonstration of fact or an adequate explanation.” 7
Is this really true as Meyer suggests? Are there no details in scientific literature regarding how the evolutionary mechanism can possibly work at higher levels of functional complexity? Certainly, I myself have found no documented “demonstrations” of evolution in action producing any qualitatively novel system that requires a minimum of more than than a few hundred specifically arranged residues – which is about the limit of evolutionary progress expected for the limited population sizes that can be maintained on this planet. However, I have recently come across at least one argument for how the sequence space problem might be overcome (already discussed briefly above).
Compensatory Mutations
Just a short time ago, in this forum, Dr. Nick Matzke argued that conversion mutations are key to solving the problem for the rarity of beneficial sequences within higher levels of sequence space (Link).
It is true that most mutations have this effect [an exponential decline in the functionality of the system for each additional mutation], but this doesn’t matter, since they happen for the most part one at a time, and (1) selection removes the severely deleterious mutations, and (2) the slightly deleterious ones can later be corrected by compensatory substitutions.
In this light, consider the following classic example of conversion mutations restoring function after a detrimental mutation:
It is well known that the folding of RNA molecules into the stem-loop structure requires base pair matching in the stem part of the molecule, and mutations occurring to one segment of the stem part will disrupt the matching, and therefore, have a deleterious effect on the folding and stability of the molecule. It has been observed that mutations in the complementary segment can rescind the deleterious effect by mutating into a base pair that matches the already mutated base, thus recovering the fitness of the original molecule (Kelley et al., 2000; Wilke et al., 2003). (Link)
Consider that every single nucleotide position could be changed in this RNA sequence, 100%, without any loss of structure or function – if done in a very precise manner. All that has to be done to maintain structure/function is to modify the opposing nucleotide to match any mutational change that happens to come along. The problem, of course is that workable compensatory mutational options are very limited. Again, the potential for 100% sequence divergence doesn’t truly reflect the sequence/structural restrictions of the system.
This nicely illustrates my observation that compensatory mutations simply don’t produce novel structures with novel functional complexity beyond very low levels of functional complexity. They simply compensate for a loss of structure/function that results from detrimental mutations by trying to get back to the original – to one degree or another. This is why compensatory mutations are so constrained. Depending upon the detrimental mutation, only a limited number of compensatory mutations are possible – and most of these do not provide full functional recovery from what was lost. In other words, the original level of functionality is not entirely reproduced by most compensatory mutations. In fact, populations tend to fix compensatory mutations only when the rate of compensatory mutations exceeds the rate of reversion or back mutations by at least an order of magnitude (Levine et. al., 2000).7 This means, of course, that back or reversion mutations are usually the most ideal solution for resolving detrimental mutations, but are not always the first to be realized by random mutations. And, compensatory mutations are usually detrimental by themselves. That means, once a compensatory mutation occurs, it is no longer beneficial to revert the original detrimental mutation (since one would also have to revert the compensatory mutation as well). This is somewhat of a problem since compensatory options are more common. That is why a compensatory mutation is usually realized before a reversion mutation – up to 70% of the time (Link). However, because compensatory mutations are not generally as good as back mutations at completely restoring the original level of functionality, they are less likely to be fixed in a population – especially larger populations.
However, the basic argument that there are a number of potential compensatory mutations for most detrimental mutations (an average of 9 or so for most proteins) is clearly correct. So then, does it not therefore follow that these compensatory options do in fact significantly expand the size of the island within sequence space and create a net-like appearance across vast regions of sequence space?
As already explained with the balloon shadow illustration, while compensatory mutational options do increase the size of the island in sequence space (by about an order of magnitude on average), this really isn’t significant given the scale of the problem at hand and the hyperdimensional nature of protein sequence space. Compensatory mutations simply expand the size of the island to the extent allowed by the specificity requirements of the system, but they do not make it possible for the island stretch out indefinitely over all of sequence space. The minimum structural threshold requirements simply will not allow this. The same basic structure with the same basic function and the same minimum number of required building blocks must be maintained. And, that puts a very restrictive size limit on the overall size of the island within sequence space (size being defined by the absolute number of protein sequences that can produce a given structure with a particular type of function). In other words, the actual maximum number of protein sequences that comprise the island is still very very limited.
Climbing Mt. Improbable
 Which leaves us back where we started. The average time it takes to get from one functional island to the next closest island in sequence space is in fact affected, quite dramatically, by the exponential decline in the ratio of potentially beneficial vs. non-beneficial sequences in sequence space with each step up the ladder of functional complexity. “Climbing Mt. Improbable” is not as easy on the “back side” of the mountain as those like Richard Dawkins seem to imagine. Why not? Because, the backside of the mountain is not comprised of small little uniform steps from the bottom to the top. Rather, the steps from the bottom to the top get exponentially larger and larger from the bottom to the top.
Which leaves us back where we started. The average time it takes to get from one functional island to the next closest island in sequence space is in fact affected, quite dramatically, by the exponential decline in the ratio of potentially beneficial vs. non-beneficial sequences in sequence space with each step up the ladder of functional complexity. “Climbing Mt. Improbable” is not as easy on the “back side” of the mountain as those like Richard Dawkins seem to imagine. Why not? Because, the backside of the mountain is not comprised of small little uniform steps from the bottom to the top. Rather, the steps from the bottom to the top get exponentially larger and larger from the bottom to the top.
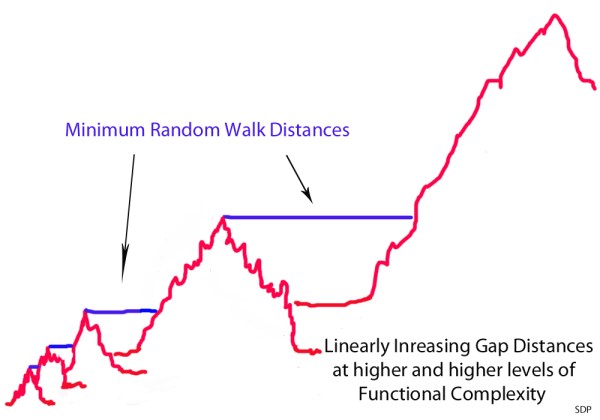
Consider, for comparison, how the climb up the mountain of functional complexity is portrayed on the Panda’s Thumb website:
 ____________________________________
____________________________________
However, in reality, this is what happens:
The minimum non-selectable Levenshtein distances between the peak of one mountain and the next closest beneficially selectable sequence with qualitatively novel functionality increases linearly with each step up the ladder of functional complexity. It’s kind of like a fractal where the the only think that changes is the scale. However, this change in scale has a dramatic effect on the average random walk time at different scales. With each linear increase in the minimum Levenshtein (or Hamming) distance, the average random walk time increases exponentially. What this means is that populations get stuck on the peaks of these mountain ranges at very low levels of functional complexity – because neutral gap distances, or otherwise non-beneficial gap distances, are simply too wide to be crossed, this side of trillions of years of time, beyond these very low levels of functional complexity.
Design Flaws
Of course, there is the final rather desperate argument that no God or any other intelligent designer would create such a nested “Tree of Life” hierarchical pattern, nor would He create so many obvious “flaws” that are evident in biological machines.
The main problem with the “design flaw” arguments is that these arguments don’t really have anything to do with explaining how the evolutionary mechanism could have done the job. Beyond this, they don’t really rule out intelligent design either because, even if someone could make it better, that doesn’t mean that an inferior design was therefore not the result of deliberate intelligence. Lots of “inferior” human designed systems are none-the-less intelligently designed. Also, since when has anyone made a better human eye than what already exists? It’s like my four year old son trying to explain to the head engineer of the team designing the Space Shuttle that he and his team aren’t doing it right. I dare say that until Richard Dawkins or anyone else can produce something as good or better themselves, that it is the height of arrogance to claim that such marvelously and beautifully functional systems are actually based on “bad design”.
 Beyond this, consider the fairly well-known arguments of Dr. Kenneth Miller (cell and molecular biologist at Brown University) who once claimed that the Type III secretory system (TTSS: a toxin injector responsible for some pretty nasty bacteria – like the ones responsible for the Bubonic Plague) is evidence against intelligent design – specifically Michael Behe’s “irreducible complexity” argument for design (Link). How so? Miller argued that the TTSS demonstrates how more complex systems, like the flagellar motility system, can be formed from more simple systems, like the TTSS since its 10 protein parts are also contained within the 50 or so protein parts, according to Miller at the time, of the flagellar motility system (actually requires a minimum of about 23 structural parts). The only problem with this argument, of course, is that it was later demonstrated that the TTSS toxin injector actually devolved from the fully formed flagellar system, not the other way around (Link). So, as it turns out, Miller’s argument against intelligent design is actually an example of a degenerative change over time – i.e., a form of devolution, not evolution. Of course, devolution is right in line with the predictions of intelligent design. Consider, for example, that it is fairly easy to take parts away from a system,
Beyond this, consider the fairly well-known arguments of Dr. Kenneth Miller (cell and molecular biologist at Brown University) who once claimed that the Type III secretory system (TTSS: a toxin injector responsible for some pretty nasty bacteria – like the ones responsible for the Bubonic Plague) is evidence against intelligent design – specifically Michael Behe’s “irreducible complexity” argument for design (Link). How so? Miller argued that the TTSS demonstrates how more complex systems, like the flagellar motility system, can be formed from more simple systems, like the TTSS since its 10 protein parts are also contained within the 50 or so protein parts, according to Miller at the time, of the flagellar motility system (actually requires a minimum of about 23 structural parts). The only problem with this argument, of course, is that it was later demonstrated that the TTSS toxin injector actually devolved from the fully formed flagellar system, not the other way around (Link). So, as it turns out, Miller’s argument against intelligent design is actually an example of a degenerative change over time – i.e., a form of devolution, not evolution. Of course, devolution is right in line with the predictions of intelligent design. Consider, for example, that it is fairly easy to take parts away from a system,  destroying the function of the more complex system (motility in the case of the bacterial flagellum) while maintaining subsystem functionality (like the T3SS toxin injector) – as originally explained by Behe (Link). It is another thing entirely to add parts to system to achieve a qualitatively new higher level system of function that requires numerous additional parts to be in a specific arrangement relative to each other before the new function can be realized to any selectable advantage. Such a scenario simply doesn’t happen beyond very low levels of functional complexity because the significant number of non-selectable non-beneficial modifications to pre-existing systems within a gene pool that would be required to achieve such a feat would take far far too long – i.e., trillions upon trillions of years. (See the following video of a lecture I gave on this topic – starting at 27:00):
destroying the function of the more complex system (motility in the case of the bacterial flagellum) while maintaining subsystem functionality (like the T3SS toxin injector) – as originally explained by Behe (Link). It is another thing entirely to add parts to system to achieve a qualitatively new higher level system of function that requires numerous additional parts to be in a specific arrangement relative to each other before the new function can be realized to any selectable advantage. Such a scenario simply doesn’t happen beyond very low levels of functional complexity because the significant number of non-selectable non-beneficial modifications to pre-existing systems within a gene pool that would be required to achieve such a feat would take far far too long – i.e., trillions upon trillions of years. (See the following video of a lecture I gave on this topic – starting at 27:00):
.
References:
- Kirk K Durston, David KY Chiu, David L Abel and Jack T Trevors, “Measuring the functional sequence complexity of proteins”, Theoretical Biology and Medical Modelling 2007, 4:47
- Bowie, J. U., & Sauer, R. T. (1989) “Identifying Determinants of Folding and Activity for a Protein of Unknown Structure”, Proceedings of the National Academy of Sciences USA 86, 2152-2156.
- Bowie, J. U., Reidhaar-Olson, J. F., Lim, W. A., & Sauer, R. T. (1990) “Deciphering the Message in Protein Sequences: Tolerance to Amino Acid Substitution”, Science 247, 1306-1310.
- Reidhaar-Olson, J. F., & Sauer, R. T. (1990) “Functionally Acceptable Substitutions in Two -Helical Regions of Repressor”, Proteins: Structure, Function, and Genetics 7, 306-316.
- R.T. Sauer, James U Bowie, John F.R. Olson, and Wendall A. Lim, 1989, ‘Proceedings of the National Academy of Science’s USA 86, 2152-2156. and 1990, March 16, Science, 247; and, Olson and R.T. Sauer, ‘Proteins: Structure, Function and Genetics’, 7:306 – 316, 1990.
- Thirumalai, D.; Klimov, D. K., Emergence of stable and fast folding protein structures, STOCHASTIC DYNAMICS AND PATTERN FORMATION IN BIOLOGICAL AND COMPLEX SYSTEMS: The APCTP Conference. AIP Conference Proceedings, Volume 501, pp. 95-111 (2000).
- Stephen C Meyer, “Darwin’s Doubt” (2013), Chap. 10, 11 – p. 185-229
- Robert M. Hazen, Patrick L. Griffin, James M. Carothers, and Jack W. Szostak, Functional information and the emergence of biocomplexity, 8574-8581| PNAS | May 15, 2007 | vol. 104 | suppl. 1
- Sean Pitman, “The Evolution of the Flagellum” (2010), Calculation (Link)
- Pallen and Matzke 2006, “From The Origin of Species to the origin of bacterial flagella.” Nature Reviews Microbiology advance online publication 5 September 2006. (Link)
- Andreas Wagner, “The Origins of Evolutionary Innovations: A Theory of Transformative Change in Living Systems” (2011), p. 64 (Link)
- Kirk K Durston, David KY Chiu, David L Abel and Jack T Trevors, “Measuring the functional sequence complexity of proteins”, Theoretical Biology and Medical Modelling 2007, 4:47
- Jesse D. Bloom, Jonathan J. Silberg, Claus O. Wilke, D. Allan Drummond, Christoph Adami, and Frances H. Arnold, Thermodynamic prediction of protein neutrality, Proc Natl Acad Sci U S A. 2005 January 18; 102(3): 606-611.
- Bruce R. Levin, Ve’ronique Parrot, and Nina Walker, “Compensatory Mutations, Antibiotic Resistance and the Population Genetics”, Genetics, 154:985-997 (March 2000).















Pingback: The Origin of Life: Common Descent or Common Design? | adventlife
Sean, I greatly enjoy your analysis of science regarding the theories of evolution versus intelligent design. Do you have an online bio or resume that shows your research, any peer-reviewed articles, etc.?
John Fleming(Quote)
View CommentSomeone has put a bio up about me that lists some of the papers I’ve had published in pathology journals (Link). Or, you can visit my website at: DetectingDesign.com where I have a short bio listed. Mostly though, my ideas on evolution vs. creation and/or design are based on my own thoughts and reading and are listed on my website, in my book, and in some of the presentations I’ve given which have been recorded and published on YouTube (linked on my website).
Sean Pitman(Quote)
View CommentPingback: Debate between Stephen Meyer and Charles Marshall | Educate Truth
Hello. I enjoy your articles very much.
I have a question (I’ve seen you closed the comments on the junk DNA article). Many evolutionists argue that the fact that the mutation frequency is high (around 150 mutations per individual) shows that most of our DNA is junk otherwise we would go extinct. What is you opinion how can a mostly functional DNA tolerate such a high level of mutations?
doncarlo(Quote)
View Comment